
It gives information about poles and zeros, which can be calculated.If the transfer function of the system is known then the output can be easily calculated.The transfer function is dependent on the System and independent on Input.Complex integral equations and differential equation converted into the simple algebraic equations (polynomial equations).mathematical modeling and mathematical equations are useful to understand the performance, characteristics, and stability of the system It is a mathematical model that gives Gain of LTI system.In this example input is values of pole, zero, and gain, zpk command is used to find out the transfer function.īelow are some of the advantages explained. The below image shows the Matlab program for the above example. The denominator is and coefficients of the denominator are 4, 5 and 7 Here numerator is 23s + 12 and the coefficient of the numerator is 23 and 12. Therefore first we need to find out numerator and denominator separately.
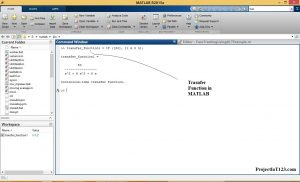
In this example, the coefficient method is used. Values of h and s are stored in the workspace. in this transfer function represented by using equation as well as ‘tf’ command is used. The above example illustrated in screen 1. In this method, we use the command “zpk”, here z stands for zeros,p stands for poles and k stands for gain.Įxample :zpk(,10) Examples & Syntax of Transfer Functions in Matlabīelow are the various examples of transfer function with their syntax: Example #1 Syntax: transfer function variable name = tf( ,)Įxample: h= tf(, 3. The numerator has only one value which is “10s”, so the coefficient is 10.Īnd in the denominator there are three terms “, so coefficients are 1, 10 and 25. In this method numerator and denominator, coefficients are used followed by ‘tf’ command. Syntax : transfer function variable name = tf(‘transfer function variable name’) In this ‘s’ is the transfer function variable.
There are three methods to obtain the Transfer function in Matlab:įirst, we need to declare ‘s’ is a transfer function then type the whole equation in the command window or Matlab editor. we consider all the initial conditions are zero because After taking Laplace Transform of the whole system, x(t) becomes X(s), y(t) becomes Y(s).

In the above system, the input is x (t) and the output is y(t). The transfer function of the LTI system is the ratio of the Laplace transform of output to the Laplace transform of input of the system by assuming all the initial conditions are zero. Hadoop, Data Science, Statistics & others Definition of Transfer Functions in Matlab


 0 kommentar(er)
0 kommentar(er)
